制限された拡散現象のMSD解析

・時刻が無限大にどうなっている？

まず，範囲を，-L/2からL/2，に制限された拡散を考えていきます．

0～L，の場合も計算できますが，この方が計算が簡単になります．

時刻が無限大の場合，粒子は-L/2からL/2の範囲で一様に分布する，と考えられますので，これを計算すればいいことになります．

初期位置を，x₀，としてまず一次元の制限された拡散の分布について考えていきます．

\( \Large \displaystyle \left< (x(t) -x_0)^2 \right> \)

が範囲内に一様に分布しているので，

\( \Large \displaystyle \left< (x(t) -x_0)^2 \right> = \frac{1}{L} \int_{-L/2}^{L/2} (x - x_0)^2 \ dx \)

\( \Large \displaystyle = \frac{1}{L} \int_{-L/2}^{L/2} (x^2 - 2x_0 x +x_0^2 ) \ dx \)

\( \Large \displaystyle = \frac{1}{L} \left[ \frac{1}{3} x^3 - x_0 x^2 +x_0^2 x\right]_{-L/2}^{L/2} \)

\( \Large \displaystyle = \frac{1}{L} \left[ \left(\frac{1}{3} \frac{L^3}{8} - x_0 \frac{L^2}{4} +x_0^2 \frac{L}{2} \right) - \left(\frac{1}{3} \frac{(-L)^3}{8} - x_0 \frac{(-L)^2}{4} +x_0^2 \frac{-L}{2} \right)\right] \)

となります．二乗の項はキャンセルされるので，

\( \Large \displaystyle = \frac{L^2}{12}+ x_0^2 \)

とシンプルになります．

ｙ方向も加えると，

\( \Large \displaystyle MSD_{ \infty} = \frac{L^2}{12}+ x_0^2 + \frac{L^2}{12}+ y_0^2 = \frac{L^2}{6}+ x_0^2 + y_0^2\)

となります．

・初期位置が中心の場合には？

もし，初期位置が中心（x₀=0, y₀=0）の場合には，

\( \Large \displaystyle MSD_{ \infty} = \frac{L^2}{6} \)

となります．

・初期位置が一様の場合には？

\( \Large \displaystyle \left< (x -x_0)^2 \right> = <x^2> - 2<x_0 x> +<x_0^2> <x^2> - 2<x_0>< x> +<x_0^2>\)

となります．ここで，初期位置，時刻が無限大には分布が一様なので，

\( \Large \displaystyle <x_0>=< x> = 0 \)

となりますので，第二項は０となります．

\( \Large \displaystyle <x^2>=< x_0^2> \)

ですので，

\( \Large \displaystyle \left< (x -x_0)^2 \right> = <x^2> + < x_0^2> = 2 \frac{1}{L} \int_{-L/2}^{L/2} x^2 \ dx\)

を計算すればいいことになります．

\( \Large \displaystyle = 2 \frac{1}{L} \left[ \frac{1}{3} x^3 \right]_{-L/2}^{L/2} = 2\frac{1}{L} \left[ \frac{L^3}{24} - \frac{(-L)^3}{24}\right] = \frac{L^2}{6}\)

となります．

ｙ方向も加えると，

\( \Large \displaystyle MSD_{ \infty} = \frac{L_x^2}{6}+\frac{L_y^2}{6} = \frac{L^2}{3} \)

となります．

興味深い点は，

　初期位置によってMSDのサチる値が異なる

ことです．たしかに，原点からの二乗変位と，ランダムな位置からランダムな位置の二乗変位，は異なることが直感的にわかります．

では，久住先生の膜タンパク質の拡散の計測は，１粒子の軌道追跡，single particle tracking，ですので，膜上の囲いがどこにあるかは不明となります．つまり，

　観測できない膜上の囲いのランダムな位置から開始した解析

なので，２次元拡散においては，L/3，が適していることになります．

ただ，グリーン関数において，どの時点で初期位置を設定したか，は．．．．すいません，私は理解できておりません．

いずれの条件においても，ｔ～０近辺では，制限された影響は少なく，自由拡散となりますので，

\( \Large \displaystyle MSD_{ t \sim 0 } = 4 D t \)

となりますが，徐々にサチって行くことになります．正確な曲線はグリーン関数を使って解いた式を用いればいいのですが．．．まあ指数関数でもいいかな？

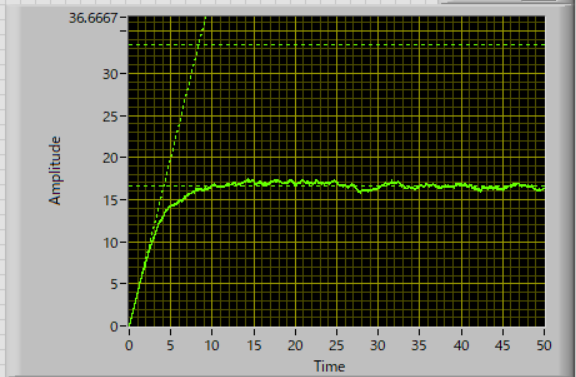
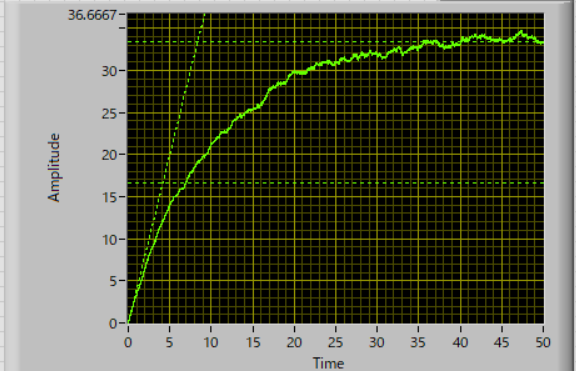
実際にシミュレーションの結果が，以下のようになります．

　　　　　　　　　　　初期位置が中心の場合　　　　　　　　　　　　　　　　　　　初期位置が均一の場合

D=1，L＝10，の計算結果なので，それぞれ，

\( \Large \displaystyle \hspace{40pt} MSD_{ center}( \infty) = \frac{L^2}{6} \sim 16.67 \hspace{120pt} MSD_{ uniform}( \infty) = \frac{L^2}{3} \sim 33.33 \)

となり，正しく表現できていることがわかります．

・シミュレーション

Youtubeに，シミュレーション動画をアップしたので，御覧ください．

長さLの平方で制限された二次元拡散のシミュレーションを行ってみました．

Program : Labview 2013
Method : Monte Carlo
Time : 50 s
dt : 0.0005 s
L : 10
D : 2
N : 1000